TEOMAPIN
DPI2008-00403.
TEOMAPIN: Solutions to the gap between Mathematical Theory and Engineering Applications in the field of Systems and Automation.
OBJECTIVES
SUMMARY
This project focuses on the intersection of Engineering, Computer Science, and Applied Mathematics. A thorough understanding of the fundamentals of practical problems allows tackling a wide variety of Engineering applications. The work area is Systems and Automation, specifically focusing on Identification, (in)validation, control, implementation analysis, diagnostics, and fault tolerance. The systems to be treated will be general: dynamic models, linear or nonlinear, continuous or discrete time, with bounded uncertainty, parametric, dynamic, or combinations of both, time-invariant or time-varying. The gap between theory and practice in this area remains open, and the focus of this project is to solve practical problems that prevent the application of new techniques to real-world situations of significant complexity and to generate (and possibly solve) theoretical problems arising from practice, i.e., the gap will be addressed, not hidden.
The development focuses on three practical applications that serve as testbeds for the results obtained. The SAC group has some experience, experimental achievements, and industrial interest in these three applications, which are:
-
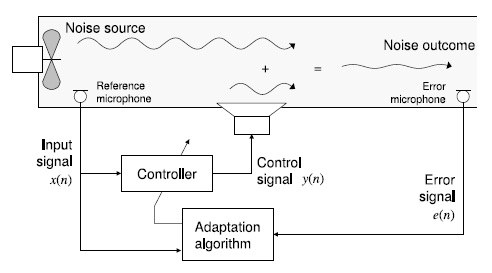
Active noise control (pipes, chambers, helmets)
-
Unmanned aerial vehicles (helicopters and airplanes)
-
Wind turbines
Work done
Determination of the position of sensors and actuators, optimized based on the maximum performance to be achieved. This objective has been approached theoretically, and the results have been applied to two different Active Noise Control problems, the motorcycle case and the acoustic duct case. One of the most significant results is a set of measures that allow comparing the quality of the sensor and actuator location based on practical performance, robustness, and controller complexity criteria.
Identification of multivariable dynamic systems (MIMO), nonlinear and/or time-varying, represented in continuous time, discrete time, or combinations of both (hybrids). Each application has brought with it restrictions and numerous gaps between theory and practice. Specifically, the identification of plants with variable delays in MIMO systems (irrigation channels) has been theoretically analyzed and practically solved, the nonlinear dynamics of acoustic noise propagation in various spaces (helmets, ducts, and boxes with windows) have been identified, and finally, the case of identification in UAVs, specifically helicopters, has been addressed, with the complexity of a multivariable, coupled, and unstable system. In this last case, a methodology has been developed that allows the application of classical techniques.
(In)validation of the previous systems against experimental data, considering variables such as external noise bounds (additive) and uncertainty (global or structured, time-varying or invariant, linear dynamic or nonlinear static). One of the most notable contributions in this framework is a robust identification/validation method for Linear Parameter Varying (LPV) models. This method allows completing nominal LPV identification algorithms by adding uncertainty and noise bounds that generate a set of models consistent with experimental evidence.
Numerical problems associated with the use of computers or DSPs in the analysis, synthesis, and implementation of controllers. The application of active control and UAV control requires real-time implementation and/or significant computational limitations that prevent the use of arbitrarily large or complex controllers. Moreover, these systems often have zeros with positive real parts and poorly damped oscillations. Therefore, designing a low-order controller is a necessity that represents a great challenge to control theory.
Determination of the most appropriate type of uncertainty to describe a physical system through a family of models and the computation of the least conservative bounds possible. Here, stability and robust and nominal performance in models with uncertain delays have been analyzed for global dynamic uncertainty structures and structured parametric uncertainty.
Most notable publications
- R. Sanchez, Y. Bolea, and V. Puig, "MIMO Smith Predictor: General Performance and Robustness results", Journal of Process Control, Vol. 19 (1), pp. 163-177, <doi:10.1016/j.jprocont.2007.12.004>, 2009.
- F. Bianchi and R. Sánchez-Peña, "Robust identification/validation in an LPV framework", International Journal of Robust and Nonlinear Control, Vol. 20 (3), pp. 301-312, <doi: 10.1002/rnc.1430>, 2010.
- F. Bianchi and R. Sánchez-Peña, "Interpolation for gain-scheduled control with guarantees", Automatica, Vol. 47 (1), pp. 239-243, <doi: 10.1016/j.automatica.2010.10.028>, 2010.
- R. Castañé-Selga and R. Sánchez-Peña, "A novel design approach for switched LPV controllers", International Journal of Control, Vol. 83 (8), pp. 1710-1717, <doi:10.1080/00207179.2010.490599>,2010.
Share: